Coating thickness

DIN EN 1071-2 (4) C

Unter Nutzung der exakten Gleichung

After having grinded a hole into the coating in that way that the base

material is visible, the coating thickness can be determined from the

ratio of the resulting circles.

Having opened this function in the menu -"Measure" the inner and outer circle

are marked each with three clicks. After three clicks the first circle is drawn

further three clicks later a window for the entry of the cutter diameter opens up.

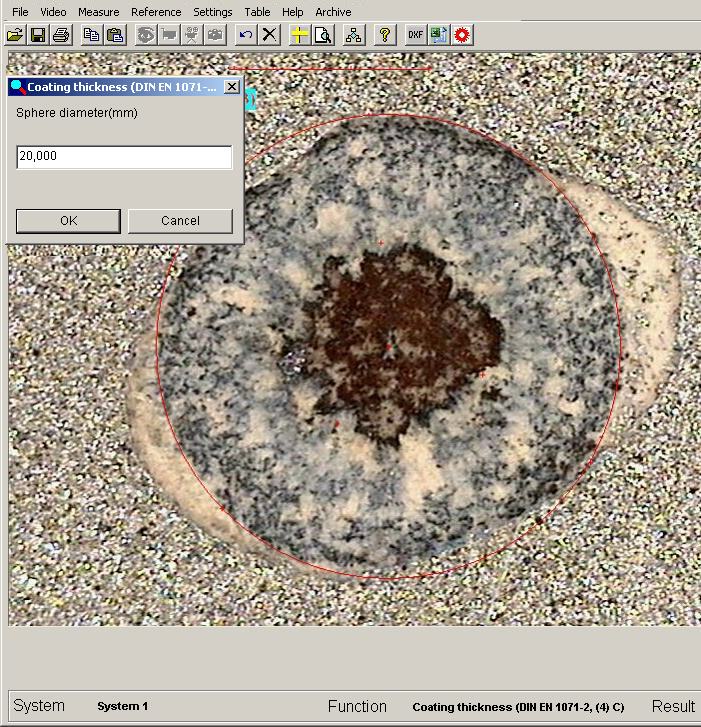
The input is closed up with OK and is checked for plausibility. When the input is proper the result appears

in the status bar.

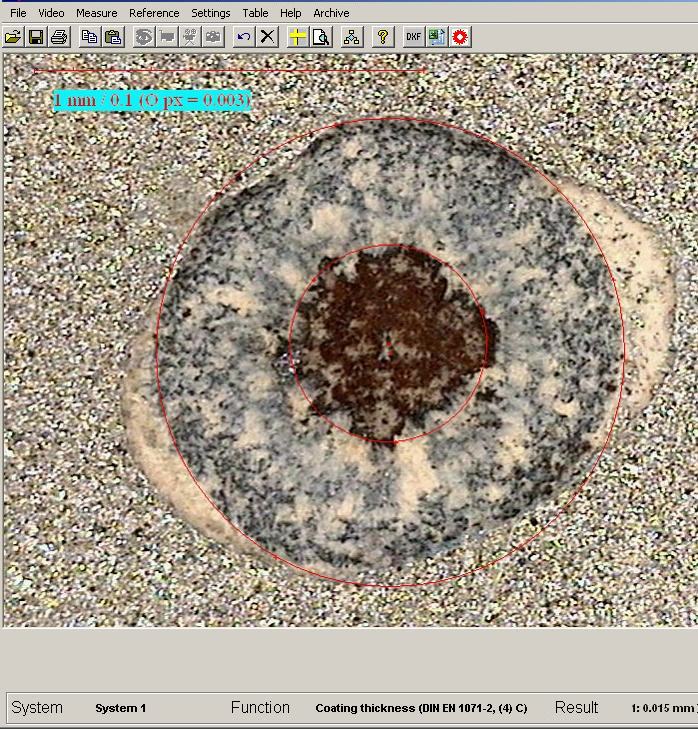
The result is prompted into the table via:

"Table" - "Enter object" or

"Ctrl + T" or

with the right mouse button (selectable in the program options)

DIN EN 1071-2 (4) L

Using the exact equation

Here the coating thickness is measured with lines. After calling up this function four points are marked

along an imaginary line from the left to the right or vise versa. After the fourth click again the window

for the input of the diameter opens up.The input is closed up with OK and is checked for plausibility.

When the input is proper the result appears in the status bar.

DIN EN 1071-2 (6) C

DIN EN 1071-2 (6) L

The only difference to the measurements mentioned above lies in the use of the approximate equation

instead of the exact eqation.The carrying out is the same as described above.

Mathematical background

DIN EN 1071-2 decribes the measurement of coating thickness using the dome-shaped process. A ball-end

mill is employed to grind through the layer to be measured and just to scratch into the material underneath.

Ideally two concentric circles emerge from that.

The geometry now shows us that the coating thickness can be calculated as following :

Naturally this equation is easy to handle for a computer, but the DIN defines also simplifications of

this equation which were helpful for the calculation without a computer. From a mathematical view

it is a Taylor expansion of the radical with termination after the first expansion. This is valid for thin

layers in comparison to the cutter diameter.

If one is dependend on the determination of lengths and can not determine diameters, two new

quantities are defined in a way that applies:

D = X + Y and d = X - Y .

This means descriptively, that X represents the width of the circular ring and Y the diameter of the

inner circle plus the width of the circular ring. These two quantities are easily to measure as a line.

The equation now becomes

This produces four possible variants:

a) Determination of the circle diameter using the exact equation

b) Determination of the lengths of the lines using the exact equation

c) Determination of the circle diameter using the approximate equation

d) Determination of the lengths of the lines using the approximate equation

These four variants are stored in Metric, to secure that the in-house comparisons on the base of

all possible variants can be kept.